Anyone who has seen John Carpenter’s Vampires, Dracula, Blade, or any other vampire film is already quite familiar with the vampire legend. The vampire needs to feed on human blood. After one has stuck his fangs into your neck and sucked you dry, you turn into a vampire yourself and carry on the blood-sucking legacy. The fact of the matter is, if vampires truly feed with even a tiny fraction of the frequency that they are depicted as doing in the movies and folklore, then humanity would have been wiped out quite quickly after the first vampire appeared.
Let us assume that a vampire needs to feed only once a month. This is certainly a highly conservative assumption,
TEAM TIP
Use behavior over time graphs to stimulate conversation around changing trends in your organization. If we were at this level a year ago, and we’re at this level today, where can we expect to be next year? What do we need to do to get there?
given any Hollywood vampire film. Now, two things happen when a vampire feeds. The human population decreases by one and the vampire population increases by one. Let us suppose that the first vampire appeared in 1600 A. D. It doesn’t really matter what date we choose for the first vampire to appear; it has little bearing on our argument. A U. S. Census web site provides an estimate of the world population for any given date. For January 1, 1600, we will accept that the global population was 536,870,911. In our argument, we had at the same time one vampire.
We will ignore the human mortality and birth rate for the time being and only concentrate on the effects of vampire feeding. On February 1, 1600, one human will have died and a new vampire will have been born. This gives two vampires and 536,870,911 – 1 humans. The next month, there are two vampires feeding, thus two humans die and two new vampires are born. This gives four vampires and 536,870,911 – 3 humans. Now on April 1, 1600, there are four vampires feeding and thus we have four human deaths and four new vampires being born. This gives us eight vampires and 536,870,911 – 7 humans.
By now, the reader has probably caught on to the progression. Each month, the number of vampires doubles so that after n months have passed, there are:
progression is known in mathematics as a geometric progression
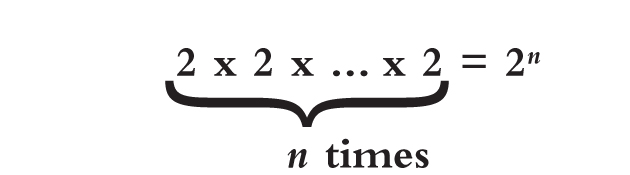
vampires. This sort of progression is known in mathematics as a geometric progression— more specifically, it is a geometric progression with ratio two, since we multiply by two at each step. A geometric progression increases at a tremendous rate, a fact that will become clear shortly. Now, all but one of these vampires were once human, so that the human population is its original population minus the number of vampires excluding the original one. So after n months have passed, there are:
536,870,911 – 2n + 1
humans. The vampire population increases geometrically, and the human population decreases geometrically (see “Change over Time in the Vampire and Human Populations”).
“Change overTime in the Vampire and Human Populations” lists the vampire and human population at the beginning of each month over a 29-month period. Note that by the 30th month, the table lists a human population of zero. We conclude that if the first vampire appeared on January 1, 1600, humanity would have been wiped out by June of 1602, two and a half years later.
CHANGE OVER TIME IN THE VAMPIRE AND HUMAN POPULATIONS
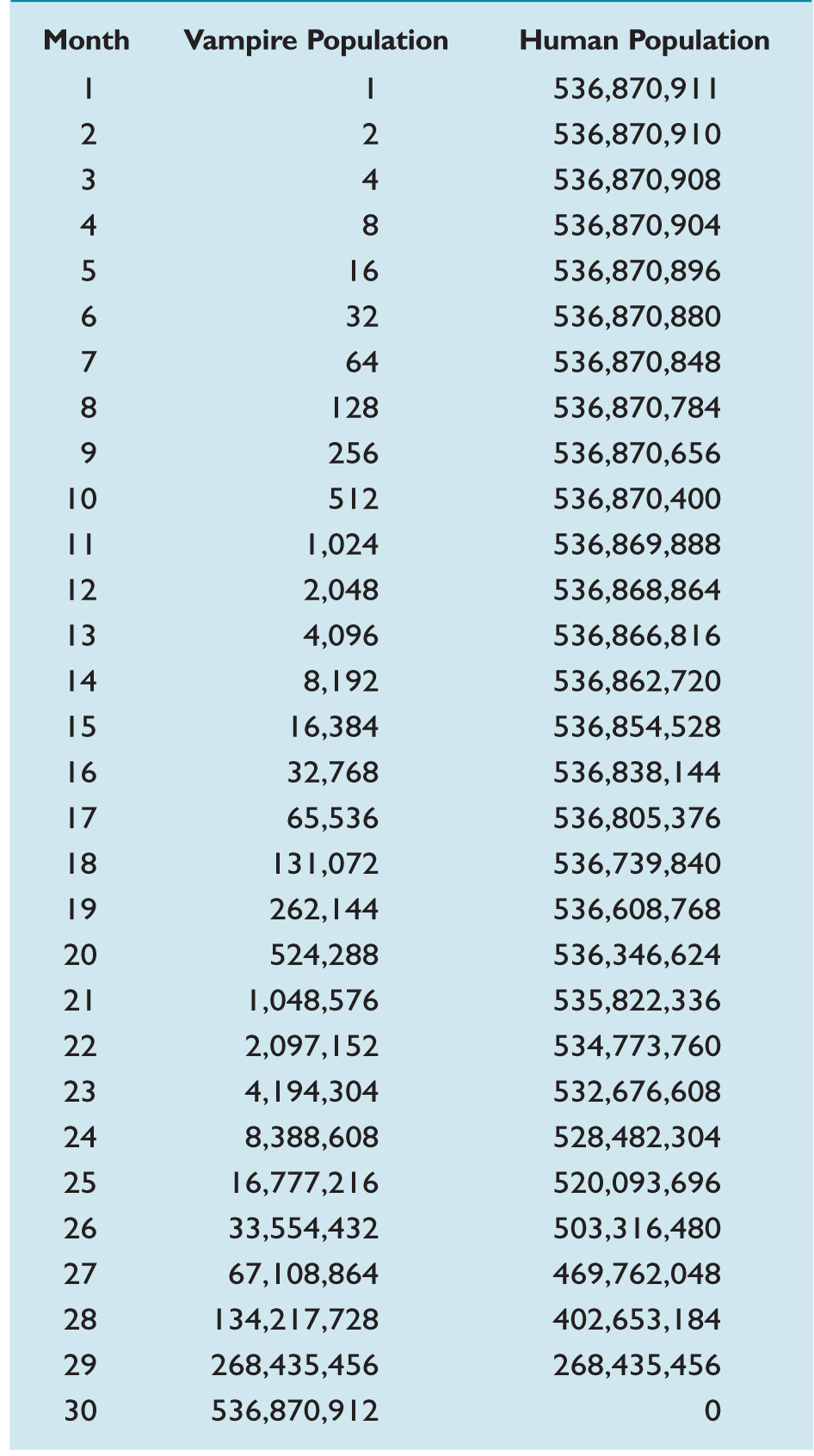
The vampire and human populations at the beginning of each month during a 29-month period.
If we factor in the human birthrate into our discussion, we find that, after a few months, the human birthrate is very small compared to the number of deaths due to vampires. This means that ignoring this factor has a negligibly small impact on our conclusion. In our example, the death of humanity would be prolonged by only one month.
We conclude that vampires cannot exist, since their existence would contradict the existence of human beings. Incidently, the logical proof that we just presented is of a type known as reductio ad absurdum, that is, “reduction to the absurd.” Another philosophical principle related to our argument is the truism given the elaborate title, the “anthropic principle.” This states that if something is necessary for human existence, then it must be true since we do exist. In the present case, the nonexistence of vampires is necessary for human existence.
Apparently, whoever devised the vampire legend had failed his college algebra and philosophy courses.
