Last weekend, the parent network in our town was buzzing. A teen in a neighboring town had invited friends over for a party while her parents were away. Before the teen knew it, 10 friends had turned into 90. The party got out of control. Crystal glasses were broken. Drawers were ransacked. Guests vomited throughout the house. The police were called.

In the end, 22 teens were arrested.

As the parent talk led to how could this happen and who was to blame, my mind turned to another question: What can we learn from this? As a systems educator, I heard a familiar pattern: small numbers escalating in unexpected and explosive ways, like invasive species, fads, and epidemics. In the story of the party, one invitation turned into two texts turned into four forwarded messages turning into eight new “friends” and so on. Sounds like exponential growth.

Most of us learn about exponential growth in a math class, somewhere between the ages of 14 and 16. We learn that exponential growth means doubling, like this: 1, 2, 4, 8, 16, 32. We learn that it’s important to know if you want your bank account to grow or if you want to understand population dynamics.

And we forget it.

So I grab a chess board, a big bag of Cheerios (jelly beans would be better), and my two boys. We read the letter-to the-editor written by the mother of the girl who threw the party.

And we talk about the numbers. How was it that one or two invitations could lead to 80 uninvited party guests?

To make it real, I put one Cheerio on the chessboard and say: “Pretend these are jelly beans. You win a bet and as your prize I have to pay you one jelly bean on the first day. For the next 63 days, I give you double the jelly beans I gave you the previous day. Sound like a good deal? There’s only one requirement: you have to agree to eat the jelly beans you get each day. Deal?”

Exponential Growth

Playing with Cheerios and exponential growth

My younger son rolls his eyes. Like, who wouldn’t accept that deal? He accepts my deal and then we walk through it:

“On the first day you get one jelly bean, the second day you get two, and on the third day you get four. So far, so good.” Now he takes over. “On the fourth day I get eight jelly beans and on the fifth I get 16 and then I get 32!”

Things are looking good. The squares are too small and the Cheerios are too big, so we pull out a piece of paper and calculate that on the 10th day, he has 512 jelly beans to eat. He’s still not fazed. Double that number on the 11th day. That would be 1,024 jelly beans.

His eyes start to widen. By the 20th day, the number is over 500,000 jelly beans. On the last day, the 64th day, he would have 18,446,744,073,709,551,616 jelly beans. He starts to look queasy. I’d DIE if I had to eat all of those jelly beans!

We draw a graph like this:

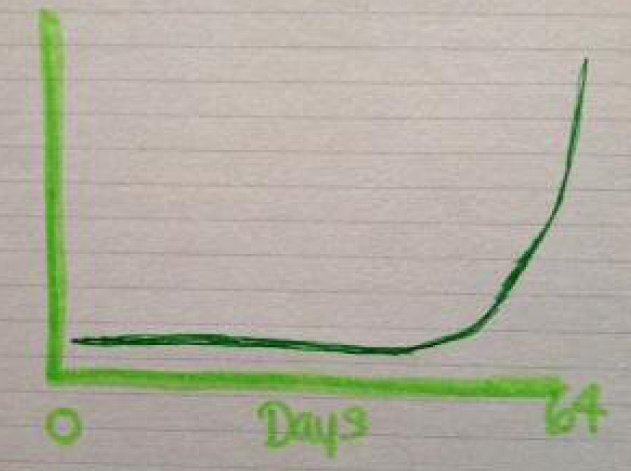
We talk about how sneaky doubling can be. And how once it gets going, in the case of the party, it can be unstoppable. “So,” I ask, trying to mask the hope in my voice, “if you understand how texting can double, could that help you avoid trouble down the road?”

Here are a couple of my kids’ answers:

Well, now I wouldn’t forward the text.

If I don’t know who the text came from in the first place, then it could already be blowing up out of control.

Of course, we also talked about not going to a party if the parents aren’t home.

My sons are 13 and 11. Will they remember this conversation when the party invitations come in as they get older? I can only hope so. Check back with me in five years and I’ll let you know.

Linda Booth Sweeney is a systems educator and is the author of numerous articles and several books, including The Systems Thinking Playbook (co-authored with Dennis Meadows) and Connected Wisdom: Living Stories about Living Systems. Linda has several children’s books coming soon; for details, “like” her Facebook page. This article originally appeared on her blog.