School superintendents, administrators, board members, and others involved in public education face a Herculean task — gaining enough understanding of an infinitely complex system so they can make good decisions about how to allocate resources; determine the impact of district, state, and federal policies on their system; and anticipate future challenges. System dynamics and computer modeling are largely untapped tools that can help decision-makers illustrate the possible results of differing policy and resource allocation decisions and unearth unintended consequences of these decisions, all in a no-risk, time-compressed environment.

Anticipating System Behavior

School districts are made up of many components, including district staff, individual schools, teachers and administrators within those schools, parent councils, and students. The sheer number and variety of these actors make it difficult to see their interdependence and to notice how an action in one part of the system affects the others. Add to this complexity policies originating from agencies outside the district, such as state education departments and the U. S. Department of Education, and the task of assessing how best to direct resources to meet students’ needs becomes almost hopelessly confusing.

Systems thinking and system dynamics tools, including casual loop diagrams, stocks and flows, and computer simulation, can shed light on the interrelationships among components and, perhaps more important, illustrate how outcomes may result from feedback loops rather than from simple, linear chains of cause and effect. These tools also make explicit the delays that often occur between a change in one component of a system and its effect on others. The interplay of feedback and delays can produce unanticipated system behavior, as shown by the mandating of smaller class sizes in California. When the legislature passed the new law, schools had to increase the number of classes they offered at each grade level to accommodate the same number of students. To do so, they needed to hire more teachers. Because becoming a teacher through traditional means requires at least four years of pre-service training, the number of teachers available fell short of meeting the needs of all schools. Suburban districts with greater resources filled their spots by recruiting teachers from urban districts, leaving those schools woefully understaffed. Proponents of the new law had failed to anticipate this unfortunate outcome of the change in class size.

By showing the potential behavior over time of multiple scenarios based on specific inputs, computer modeling offers policymakers and administrators the ability to visualize the long-term effects of specific decisions before those decisions are implemented. We can also use models to identify unexpected interactions between system components; ask “what if questions about changes in system parameters; run no-cost experiments that compress time and space; and reflect on, expose, test, and improve the mental models upon which we rely to make decisions about difficult problems. Thus, computer modeling could allow school-system leaders to make more effective decisions by building their understanding of long-term consequences of resource decisions in a complex environment.

Evaluating Professional Development Programs

To illustrate how a district can use computer modeling to analyze its options, I have created a simulation that explores the impact of professional development programs for teachers. Many school districts have responded to the call for better educational performance by implementing a standards-based curriculum. They offer professional development workshops to increase teachers’ ability to communicate this new curriculum to their students. The workshops are often formatted as multi-week summer programs.

Research has shown that teachers can learn to communicate the new curriculum through professional development training, so the question for a district is not whether summer workshops can build capacity, but whether they can do so for a critical mass of teachers in a reasonable time period. What factors play a role in this issue? Which workshops are most effective? What are the costs associated with this form of professional development? These questions are amenable to modeling because we can determine quantitative values for most of the important variables — such as the number of teachers in training and the turnover rate of teachers — and reasonable estimates for the qualitative variables — such as the effectiveness of the workshops and the relationship between the length of the workshop and the willingness of teachers to enroll in it.

I followed these steps to build the model:

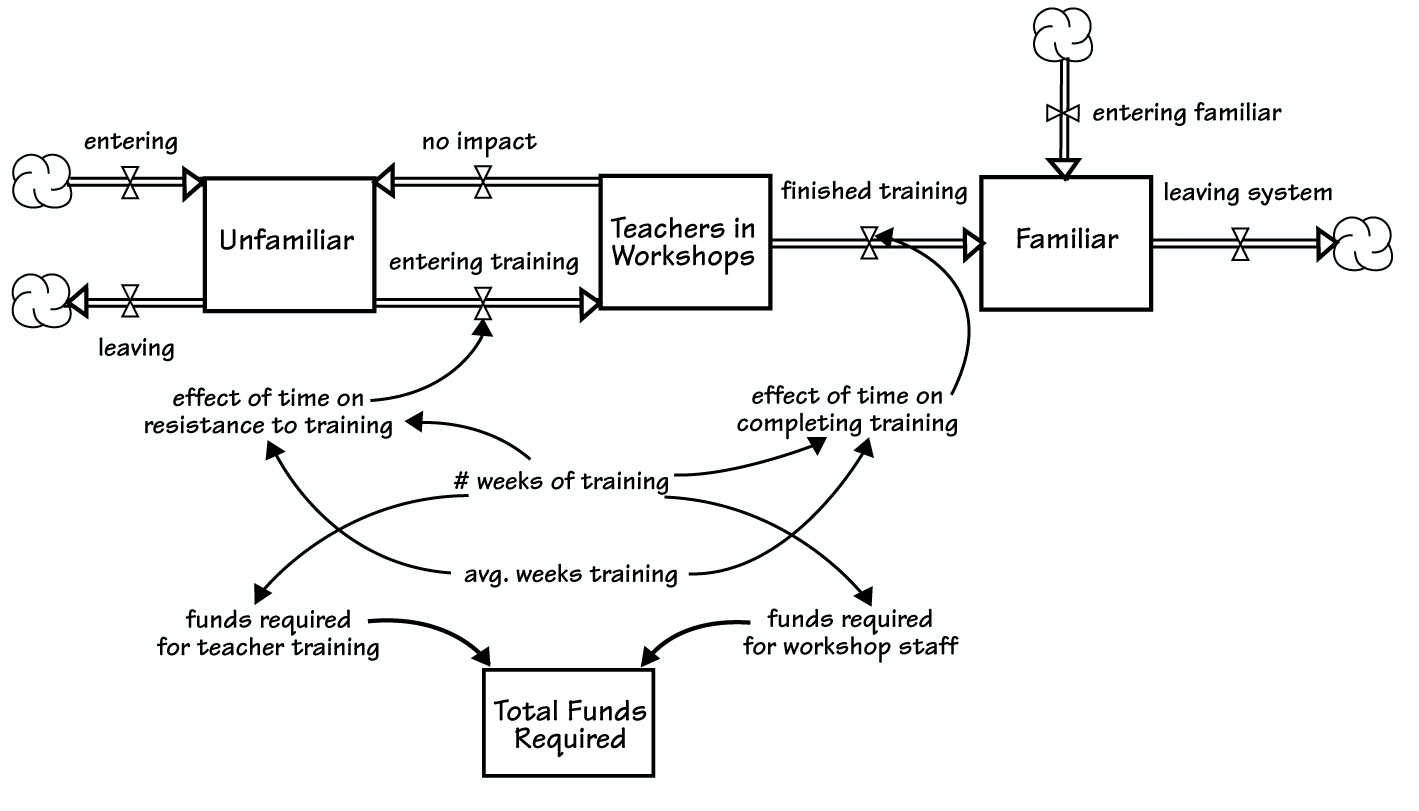
1. Define the teacher stocks. All the teachers in the district fall into three stocks: Those who are not familiar with the standards; those who are attending a workshop to learn about the standards; and those who are familiar with the standards.

2. Establish the flow between stocks. Teachers who aren’t familiar with the standards can take a workshop to gain familiarity; teachers in the workshop may become familiar with the standards and move into the “familiar” stock or may not gain much from the workshop and return to the “unfamiliar” stock; and both “familiar” and “unfamiliar” teachers may leave the system each year.

3. Identify and assign values to the important system parameters and variables.

4. Incorporate funding components.

The model is based on the following assumptions:

• The number of teachers in the system remains constant at 10,000, and at the starting point, 10 percent of the teachers are already familiar with the standards-based curriculum. Workshops vary in length from one day to five weeks.
• Ten percent of the teachers leave and are replaced each year (with 10 percent of new teachers entering in the “familiar” stage), and the rate at which teachers leave the system is higher for teachers in the “unfamiliar” pool than in the “familiar” pool.
• In the baseline simulation, 1,000 teachers participate in the three-week workshop; this number can vary up or down by a factor of three.
• Fewer teachers participate in longer workshops, more in shorter ones. However, longer workshops are more effective. The initial success rate for teachers reaching the “familiar-with-standards” stage in a three-week workshop is 30 percent. This base rate increases linearly over time as more and more teachers (those for whom training was not effective the first time) retake the workshop.
• There are 25 teachers in each workshop. The cost of the workshop includes a stipend of $300/week/ teacher for each of 25 participating teachers and an additional cost of $2,500/week for the instructor, supplies, and space.

“Modeling Professional Development” illustrates the model’s basic features.

Analyzing Results

The simulation yields several non-intuitive results, the most important being that these workshops alone cannot adequately deal with the problem of building the necessary capacity in the teacher workforce. Even after 10 years of providing three-week workshops, only 52 percent of the teachers are skilled in presenting a standards-based curriculum — and this number includes teachers who were capable before they enrolled in the workshops. The results clearly show that the workshops do not produce a critical mass of teachers with the desired capabilities in a reasonable amount of time.

Another unexpected result of this analysis is that the five-week workshops result in the largest number of trained teachers over a 10-year period, even though the smallest number of teachers enrolls in them. Holding all else constant, approximately 5,200 teachers achieve the desired level of ability after participating in a five-week workshop, while only about 2,800 teachers reach this stage through one week workshops. The longer workshop is also the most cost-effective per teacher trained: $2,300 per teacher for a five-week workshop; $2,635 for a three-week workshop; and $3,100 for a one-week workshop.

We can generalize this kind of model to other areas of professional development, because the results are independent of the workshop content. Administrators have access to the quantitative data for their district (such as number of teachers in the system, distribution by length of service, teacher leaving rate, funding available for workshops) and can reasonably estimate values for the qualitative variables (such as percent of teachers who require specific professional development, workshop effectiveness, relationship of workshop length to teacher resistance and workshop effectiveness) from prior experience. Plugging these numbers into a computer simulation would give them a general tool for predicting the impact of a summer workshop on professional development in any content area.

Similar models could let stakeholders examine other questions, such as the impact of rationing workshop participation depending on teachers’ average time of service in the system.

Should administrators concentrate on those who will remain in the system longest, that is, younger teachers? Or is there value in offering training opportunities to experienced teachers, who can serve as opinion leaders in changing the system’s culture? This analysis could also be incorporated into an expanded model to include the use of mentors and school and web-based professional development. By exploring these variables as well, districts might come upon a formula for producing a multi-component professional development system with the capacity to bring a critical mass of teachers up to speed on new curriculum requirements in an acceptable time period.

As I hope I’ve shown here, computer modeling offers a valuable planning and decision-support tool for school districts. This approach permits “no-risk” analysis of competing policy choices and resource allocations and, while it does not offer definitive answers, it can help school-system leaders understand the impact of their decisions and guide them toward making better-informed allocations of scarce resources.

Daniel D. Burke, Ph. D., has a broad understanding of K-graduate educational systems. As deputy director for education, the CNA Corporation (CNAC), he leads the research and analysis activities of CNAC’s public education group. Before joining CNAC, Dan was a researcher in molecular biology and produced an extensive record of curriculum innovations. He also played an important role in the National Science Foundation’s K-12 education reform programs.